Calculus Optimization Worksheet A Rain Gutter Is To Be Constructed

The parts for each smartphone cost 50 and the labor and overhead for running the plant cost 6000 per day.

Calculus optimization worksheet a rain gutter is to be constructed.

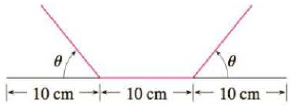
To calculate the area split the cross section of the gutter into two triangles and a rectangle. Optimization problems name calculus ab for each of the following define your variables write an equation representing the quantity to be maximized or minimized and solve the problem. How should θ be chosen so that the gutter will carry the maximum amount of water. A rain gutter is to be constructed from a metal sheet of width 30cm by bending up one third of the sheet on each side by an angle theta from the horizontal theta zero represents the unbent sheet.

You da real mvps. We have step by step solutions for your textbooks written by bartleby experts. A rain gutter is to be constructed from a metal sheet of width 30 cm by bending up one third of the sheet on each side through an angle θ. Maximizing or minimizing some quantity so as to optimize some outcome calculus is the principal tool in finding the best solutions to these practical problems.

Verify if it is a maximum or minimum using the 2nd derivative test when easy otherwise use the 1st derivative test. Most real world problems are concerned with. A rain gutter is to be constructed from a metal sheet of width 30 cm by bending up one third of the sheet on each side through an angle theta. Here are the steps in the optimization problem solving process.

1 draw a diagram depicting the problem scenario but show only the essentials. Differential calculus published in vacaville california usa a rain gutter is to be constructed from a metal sheet of width 30 cm. 1 a company has started selling a new type of smartphone at the price of 110 0 05 x where x is the number of smartphones manufactured per day. 1 per month helps.

We need to begin by constructing a function which gives the area of the gutter in terms of theta. Thanks to all of you who support me on patreon. How should theta be chosen so that the gutter will carry the maximum amount of water. Optimization problems practice solve each optimization problem.